Scalable Heterogeneous Graph Neural Networks for Predicting High-potential Early-stage Startups

Abstract

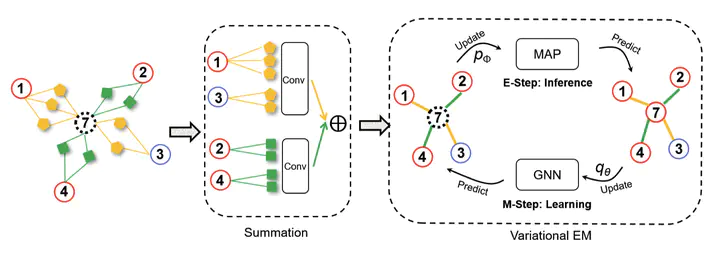
It is critical and important for venture investors to find high-potential startups at their early stages. Indeed, many efforts have been made to study the key factors for the success of startups through the topological analysis of the heterogeneous information network of people, startup, and venture firms or representation learning of latent startup profile features. However, the existing topological analysis lacks an in-depth understanding of heterogeneous information. Also, the approach based on representation learning heavily relies on domain-specific knowledge for feature selections. Instead, in this paper, we propose a Scalable Heterogeneous Graph Markov Neural Network (SHGMNN) for identifying the high-potential startups. The general idea is to use graph neural networks (GNN) to learn effective startup representations through end-to-end efficient training and model the label dependency among startups through Maximum A Posterior (MAP) inference. Specifically, we first define different metapaths to capture various semantics over the heterogeneous information network (HIN) and aggregate all semantic information into a summated graph structure. To predict the highpotential early-stage startups, we introduce GNN to diffuse the information over the summated graph. We then adopt an MAP inference over Hinge-Loss Markov Random Fields to enforce label dependency. Here, a pseudolikelihood variational expectationmaximization (EM) framework is incorporated to optimize both MAP inference and GNN iteratively: The E-step calculates the inference, and the M-step updates the GNN. For efficiency concerns, we develop a GNN with a lightweight linear diffusion architecture to perform graph propagation over web-scale heterogeneous information networks. Finally, extensive experiments and case studies on real-world datasets demonstrate the superiority of SHGMNN.